

RESITENCIA DE MATERIALES II
INTRODUCCION
El método de área de momento nos proporciona un procedimiento semigrafico para encontrar la pendiente y el desplazamiento en puntos específicos sobre la curva elástica de una viga o flecha. La aplicación del método requiere el cálculo de áreas asociadas con el diagrama de momento flector de la viga.
Cuando la viga esta inicialmente recta, es deformada elásticamente por las cargas , de modo que la pendiente y la deflexión de la curva elástica son muy pequeñas y las deformaciones son causadas por flexión.
Como todo método, nos proporciona diferentes alternativas o maneras distintas de dar solución a nuestro problema, en este caso este método de área de momento se basa en dos teoremas usados para determinar la pendiente y el desplazamiento en un punto sobre la curva elástica.
METODO DE AREA DE MOMENTO
Este método, comprende dos teoremas:
1.-El ángulo o cambio de pendiente entre las tangentes en dos puntos cualesquiera de una elástica continua es igual a la área del diagrama M/EI comprendido entre dichos puntos.
2.-La distancia de un punto B’ de una elástica continua medida perpendicularmente al eje primitivo AB a la tangente trazada por otro punto A’ de dicha curva es igual al momento respecto a B del área del diagrama M/EI comprendido entre dichos puntos.
Pasos a seguir para la aplicación del método de área – momento:
- determine las reacciones en los soportes y dibuje el diagrama M/EI de la viga. si la viga esta cargada con fuerzas concentradas, el diagrama M/EI consistirá en una serie de segmentos de líneas rectas y las áreas y sus momentos requeridos en los teoremas de área-momento serán relativamente fáciles de calcular. Si la carga consiste en una serie de cargas distribuidas, el diagrama M/EI consistirá en curvas parabólicas o tal ves en curvas de orden superior y se sugiere utilizar las tablas adecuadas para localizar el área y centroide bajo cada curva.
- Dibuje una vista exagerada de la curva elástica de la viga. Debiendo recordar siempre que puntos de pendiente y desplazamiento cero ocurren siempre en empotramientos, y que los puntos de desplazamiento cero ocurren en soportes de pasador o de rodillo. Si la viga esta sometida a un momento positivo, la viga se flexiona con concavidad hacia arriba y si esta sometida a un momento negativo, se flexiona con concavidad hacia abajo.
- El desplazamiento y la pendiente desconocida que van a determinarse, deben indicarse sobre la curva. Como los teoremas área-momento se aplican solo entre dos tangentes, debe darse atención a que tangentes deben trazarse sobre la curva para que los ángulos o desviaciones entre ellas conduzcan a la solución del problema. Respecto a esto deben considerarse las tangentes en los puntos de pendiente y desplazamiento desconocido y en los soportes, ya que la viga por lo regular tiene desplazamiento cero y/o pendiente cero en los soportes.
- Aplique el teorema “1” para determinar el Angulo entre dos tangentes cualesquiera sobre la curva elástica y el teorema “2” para determinar la desviación tangencial.
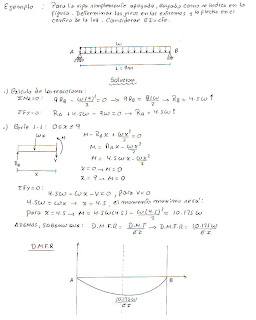
Veamos algunos ejemplos:


Conclusiones
Este trabajo nos permite tener una visión acerca de los problemas comunes que soportan las diferentes estructuras, en especial las vigas. Estos elementos estructurales soportan cargas constantes a lo largo de su vida útil los cuales son transmitidos a las columnas para luego distribuirse en las zapatas y por ultimo al suelo.
Pudimos apreciar en el trabajo como se dan las diferentes deformaciones en una viga, así mismo hemos aprendido a utilizar los dos métodos los cuales nos sirven para determinar las pendientes y giros en una viga.
Finalmente podemos concluir en que este curso nos permite asimilar la teoría con la vida real, sabiendo el porque de las cosas, la importancia que tiene el hacer un muy buen calculo, entre otras cosas.
RECOMENDACIONES
Se recomienda que el alumno tome mucho interes en el curso ya que nos estamos formando para ser unos buenos ingenieros.
El alumno debe estudiar de una manera minuciosa las diferentes deformaciones que pueda producirse en un elemento estructural, ya que eso le servirá para tener una mejor visión de las cosas que haga en el futuro.
Se recomienda que el alumno al estudiar el curso , realice visitas a obras para que así pueda ampliar en la realida sus conocimientos del tema y de esa manera se le quedara grabado algunas cosas para el futuro ( previa orientación de una persona con mucha mayor experiencia para un mejor entendimiento).










No hay comentarios:
Publicar un comentario